深度学习笔记4-循环神经网络RNN

4.1 循环神经网络

4.1.1 序列模型

序列模型：自然语言、音频、视频等序列数据的模型

应用：语音识别、情感分类、机器翻译等

为什么不使用CNN？

序列数据的前后之间具有强关联性
输入输出长度不固定

4.1.2 循环神经网络

循环（递归）神经网络（Recurrent Neural Network，RNN）是神经网络的一种，将“状态”在自身网络中循环传递，可以接受时间序列结构输入

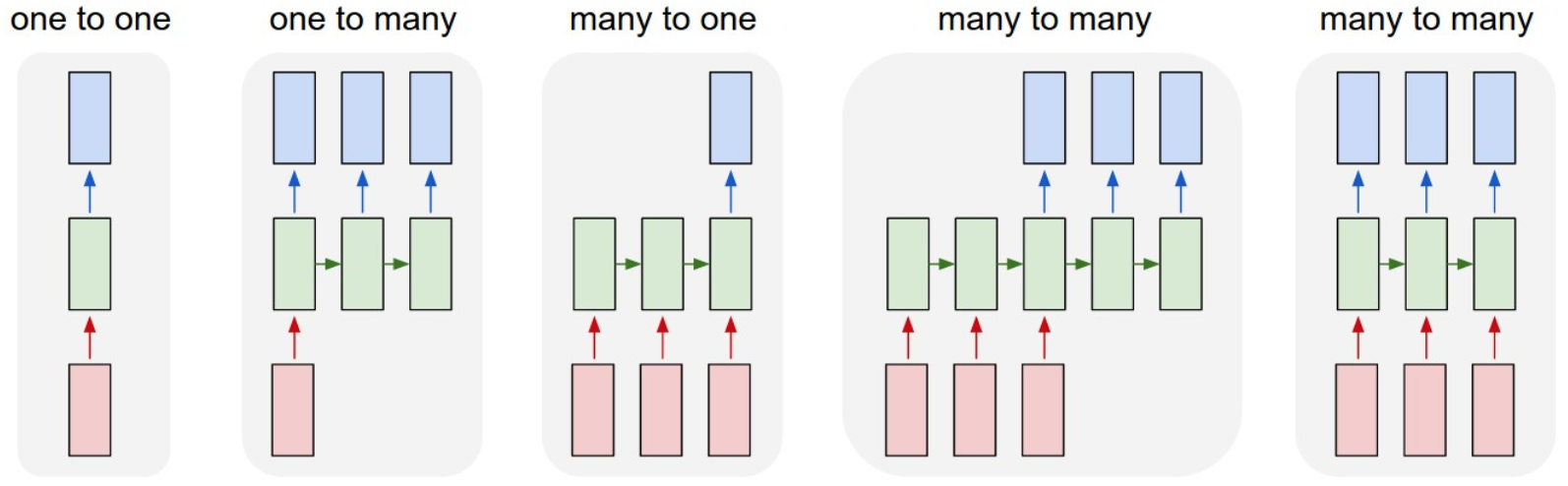
4.1.2.1 RNN类型

RNN结构

一对一：固定输入到固定输出，如图像分类
一对多：固定输入到序列输出，如图像的文字描述
多对一：序列输入到固定输出，如情感分类
（异步）多对多：序列输入到序列输出，如机器翻译，称为Encoder-Decoder（编码-解码）结构
同步多对多：同步序列到同步输出，如文本生成、视频帧分类

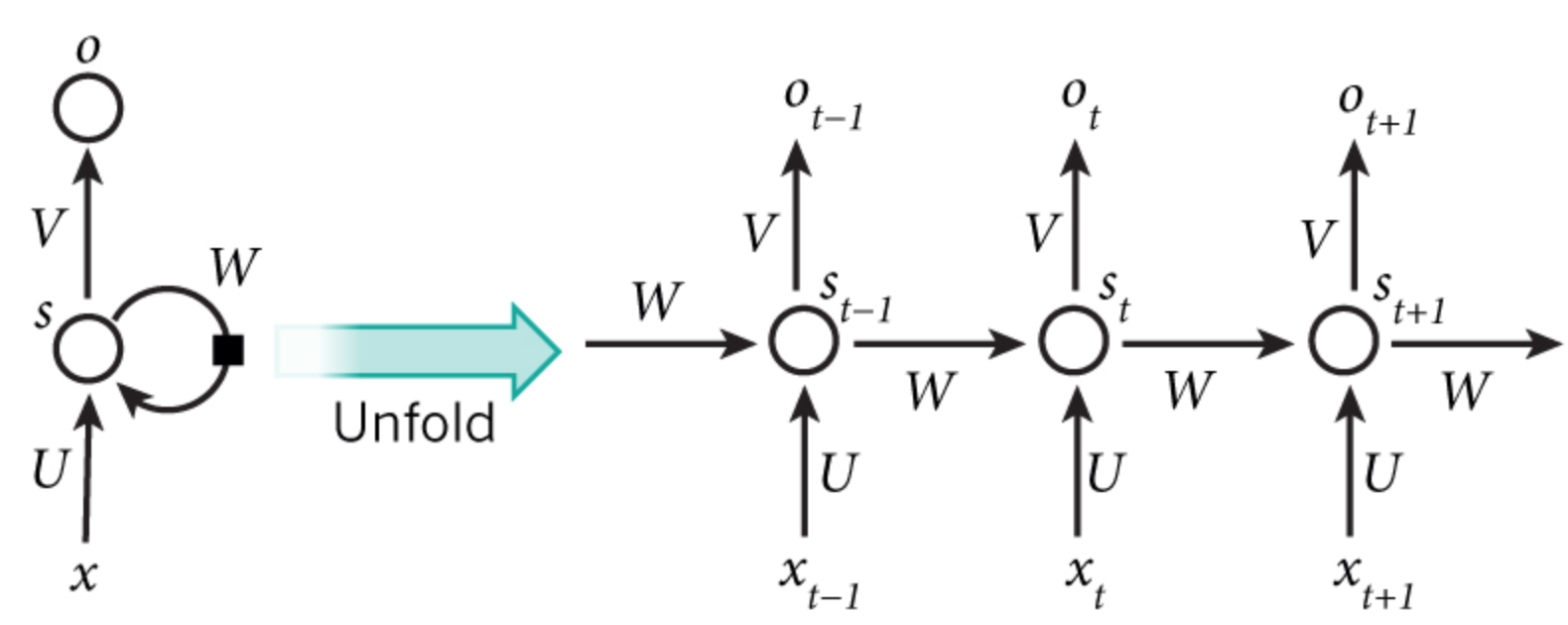
4.1.2.2 基础循环神经网络

基础RNN结构

$x_t$：t时刻的输入
$o_t$：t时刻的输出
$s_t$：t时刻的隐层输出
所有单元的参数$U, V, W$共享

统一公式（$f$采用TanH/RuLU，$g$采用Softmax/Sigmoid）：

$$
\begin{split}
& s_0 = 0 \\
& s_t = f(Ux_t + Ws_{t-1}) \\
& o_t = g(Vs_t)
\end{split}
$$

输出的$o_t$受前面时刻的隐层$s_{t-1}$影响，即RNN具有记忆功能

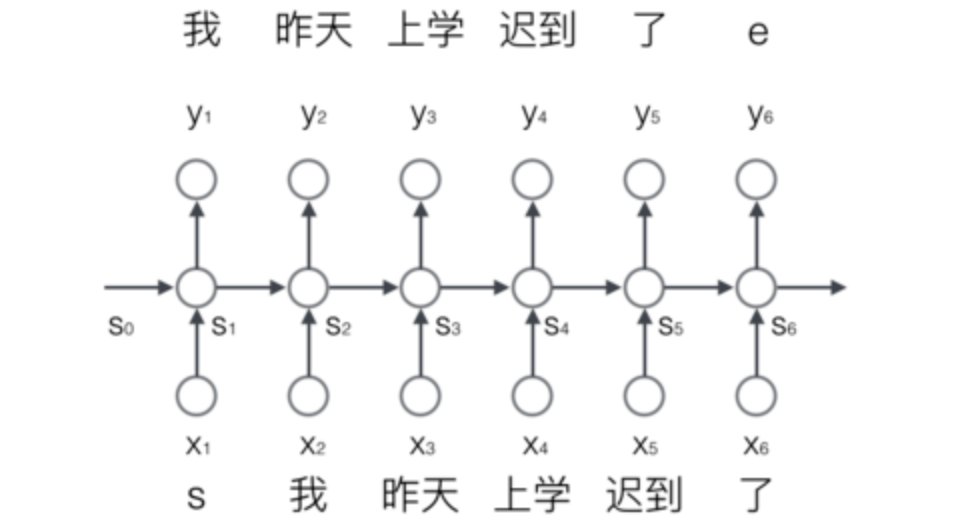
4.1.2.3 序列生成案例

序列例子

输入到网络当中的是一个个的分词结果，每一个词的输入是一个时刻
每一个时刻有一个输出，表示最可能的下一个词

4.1.2.4 词的表示

为了能够让网络理解输入，需要将词进行向量表示。

建立一个包含所有序列词的词典，每个词在词典中有唯一编号
记词典大小为$N$，任意一个词都可以用一个$N$维的One-Hot向量表示
得到一个高维稀疏矩阵

词向量表示

4.1.2.4 输出的表示-Softmax

RNN这种模型，每一个时刻的输出是下一个最可能的词，可以用概率表示，总长度为词的总数长度

每个时刻的隐层输出$s_t$经过Softmax函数，得到概率分布

4.1.2.5 交叉熵损失

总损失定义：一整个序列（一个句子）作为一个训练实例，总误差是各个时刻误差的和

$$
\begin{split}
& E_t(y_t, \hat{y}_t) = -y_t \log(\hat{y}_t) \\
& E(y, \hat{y}) = \sum_t E_t(y_t, \hat{y}_t) = -\sum_t y_t \log(\hat{y}_t)
\end{split}
$$

$y_t$：时刻t上正确的输出
$\hat{y}_t$：时刻t上预测的输出

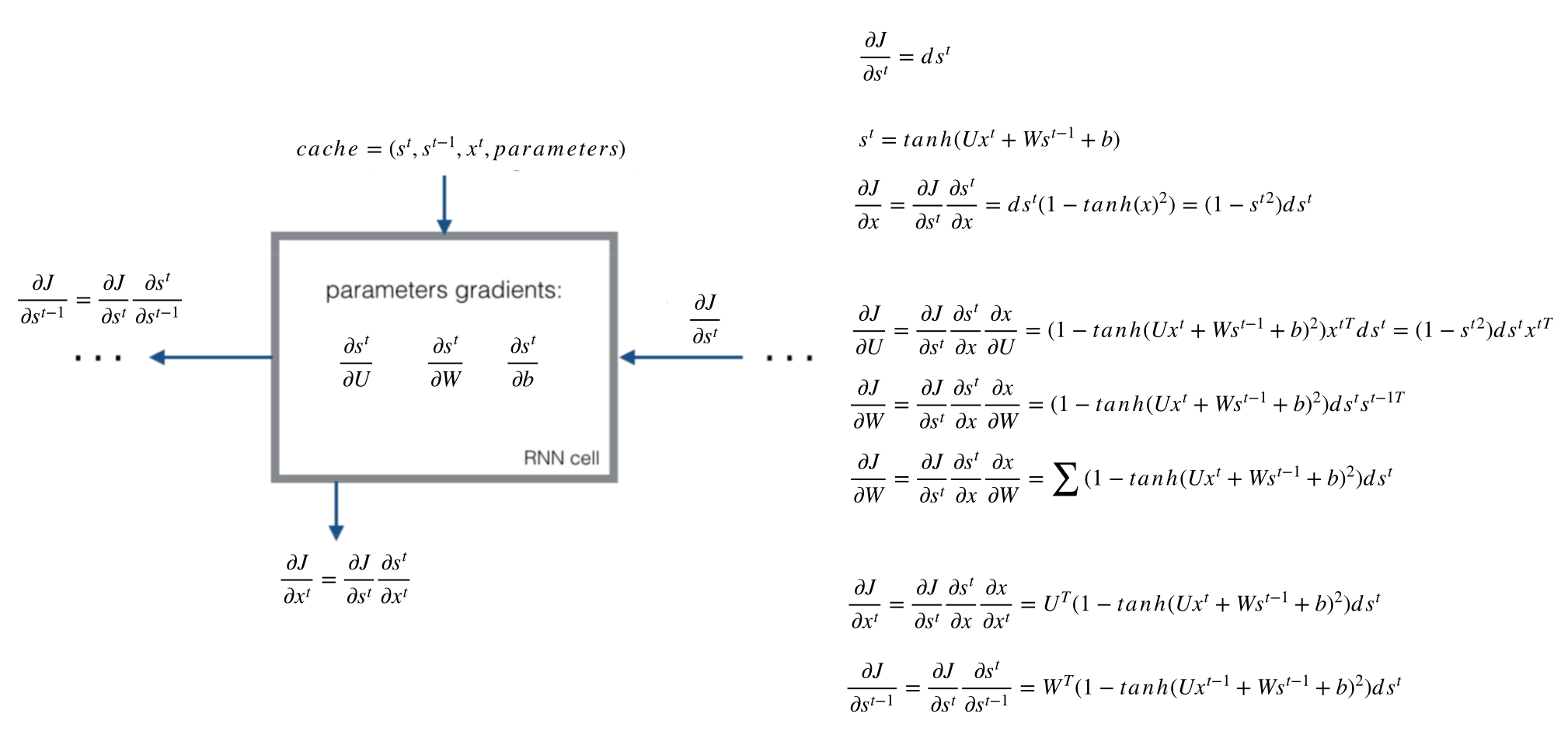
4.1.2.6 时序反向传播算法（BPTT）

Backpropagation Through Time，时序反向传播算法：对于RNN有一个时间概念，需要把梯度沿时间通道进行反向传播

需要更新的参数：$U, V, W, b_x, b_y$

计算每个时间的梯度$dW_t$，相加作为每次$W$更新的梯度值
$s_t=tanh(Ux_t+Ws_{t-1}+b_x)$，$o_t=Softmax(Vs_t+b_y)$
利用链式法则，计算出每个时间下各参数的梯度

RNN反向传播总结

4.1.2.7 梯度消失与梯度爆炸

由于RNN中也存在链式求导法则，因此也会发生梯度消失与梯度爆炸的问题

4.1.8 RNN改进

通过门控机制控制信息的流动

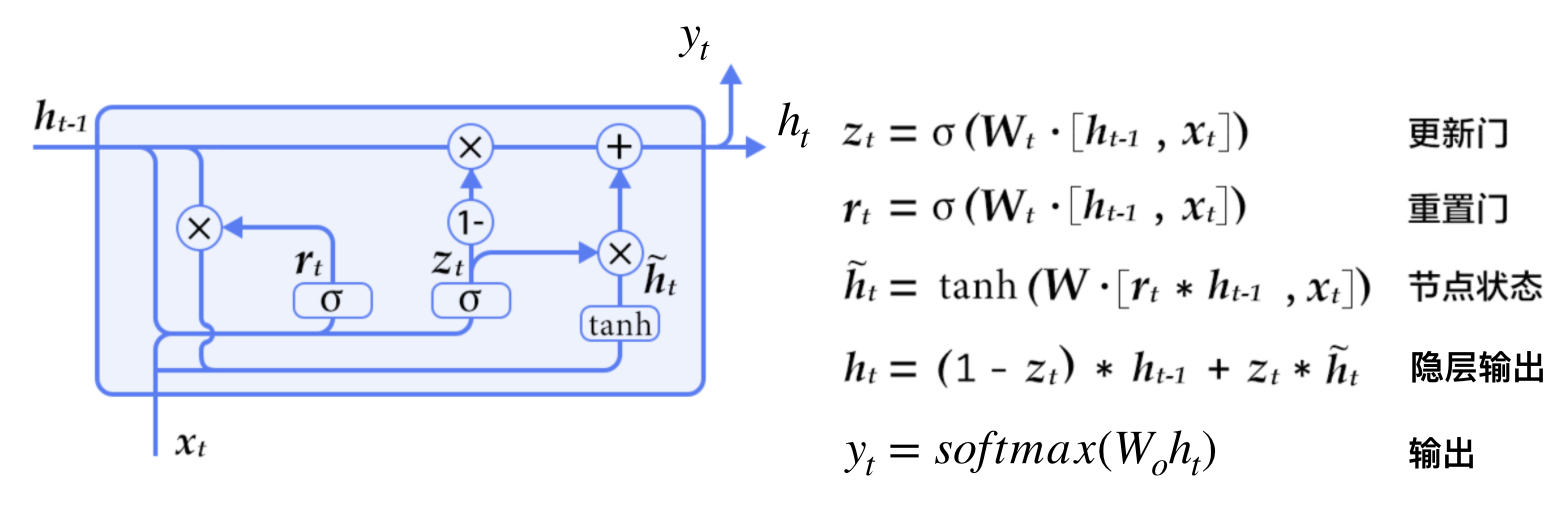
4.1.8.1 门控循环单元GRU

Gated Recurrent Unit，门控循环单元

GRU单元

GRU增加了两个门，一个重置门（reset gate）和一个更新门（update gate）

重置门：决定如何将新的输入和前一时刻的输出相结合
更新门：定义前面的记忆保存到当前时间的量
重置门1，更新门0，即为标准RNN模型

GRU本质解决的问题：

解决短期问题，每个递归单元能够自适应捕捉不同尺度的依赖关系
处理了隐层输出，$h_t=(1-z_t)h_{t-1}+z_t\tilde{h}_t$，解决了梯度消失问题

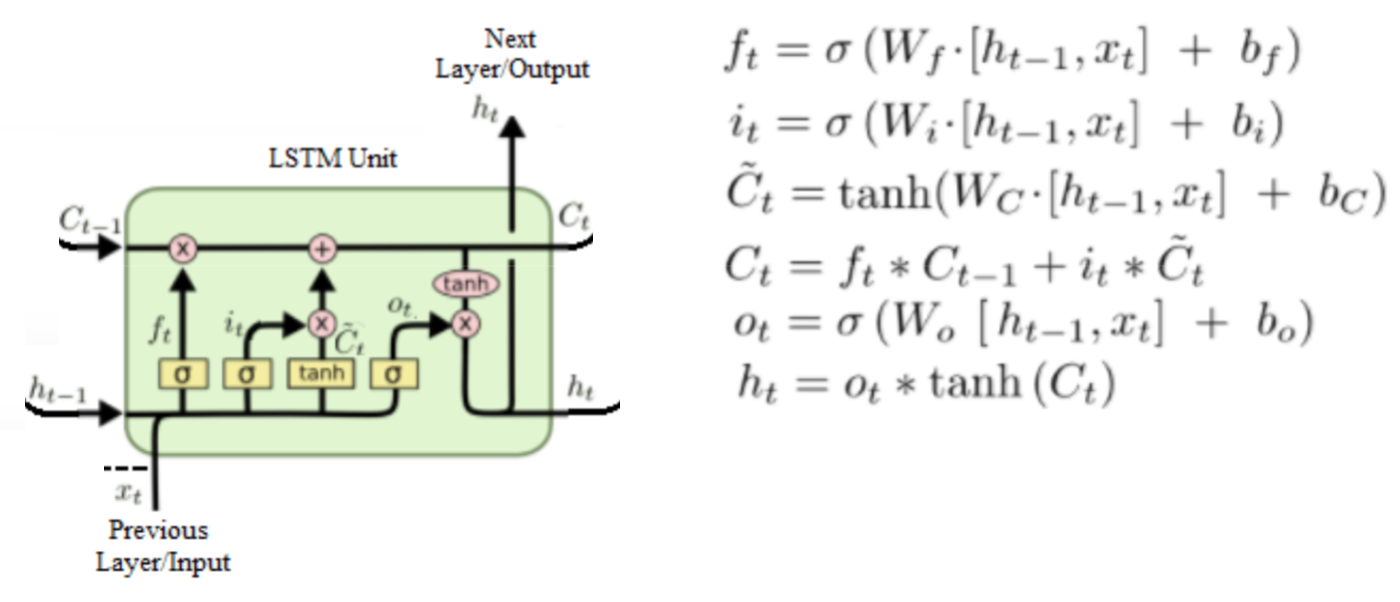
4.1.8.2 长短时记忆网络LSTM

Long Short Term Memory，长短记忆网络

LSTM

$h_t$：当前cell的输出
$c_t$：隐层的记忆
三个门：遗忘门f，输入门u，输出门o

作用：便于记忆长更长距离的状态

4.2 词嵌入与NLP

4.2.1 在RNN中使用one-hot表示的问题

假设有n个词，每个词的one-hot表示是n维的，整体大小为$n*n$，非常稀疏
无法表示词之间的相似性，例如Apple对Banana的相似性远高于Monkey

4.2.2 词嵌入（Word Embedding）

把一个维数为$N$的高维空间嵌入到一个维数低的多的连续向量空间中，每个单词或词组被映射为实数域上的向量，例如：

	Man	Woman	King	Queen	Apple	Banana
Gender	1	-1	-0.95	0.97	0.01	-0.02
Royal	0.01	0.02	0.98	0.99	-0.03	0.04
Age	0.01	0.02	0.75	0.69	0.03	-0.04
Food	0.01	0.02	-0.03	0.04	0.95	0.97

词嵌入的特点：能够体现词与词之间的关系

Man-Woman≈King-?(Queen!)

算法/工具：Skip-gram、CBOW、GenSim

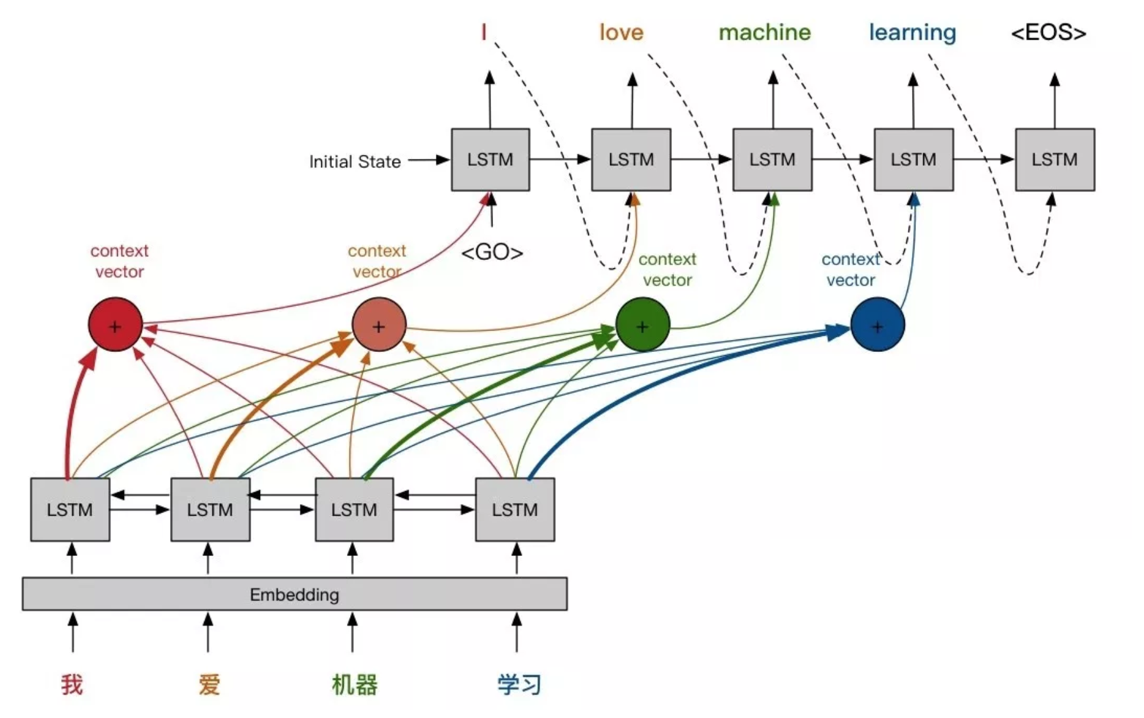
4.3 Seq2Seq与Attention机制

4.3.1 Seq2Seq

Seq2Seq：Sequence to Sequence，由Google Brain团队和Yoshua Bengio 两个团队各自独立的提出来

4.3.1.1 定义

Seq2Seq模型是一个Encoder-Decoder结构的模型，输入是一个序列，输出也是一个序列

Encoder中将一个可变长度的信号序列变为固定长度的向量表达，
Decoder中将这个固定长度的向量表达变为可变长度的目标信号序列

seq2seq

相当于把RNN模型的$s_0$输入变成一个Encoder

4.3.1.2 条件语言模型

Encoder编码器的作用：

将一个边长输入序列输出到一个编码状态$C$
解码器输出$y_t$的条件概率基于之前的输出序列$y_1y_2…y_{t-1}$和编码状态$C$
$argmaxP(y_1,y_2,…,y_T|x_1,x_2,…,x_T)$，给定输入的序列，最大化输出序列的概率

根据最大似然估计，最大化输出序列的概率

$$
\begin{split}
& P(y_1,y_2,…,y_T|x_1,x_2,…,x_T) \\
& = \prod_{t=1}^T P(y_t|y_1,y_2,…,y_{t-1},x_1,x_2,…,x_T) \\
& = \prod_{t=1}^T P(y_t|y_1,y_2,…,y_{t-1},C)
\end{split}
$$

这个公式需要求出$P(y_1|C),P(y_2|y_1,C),…,P(y_T|y_1,y_2,…,y_{T-1},C)$，概率连乘极小，不利于存储，因此取对数进行计算，这样就将连乘式转换为累加式

$$
\log P(y_1,y_2,…,y_T|x_1,x_2,…,x_T) = \sum_{t=1}^T \log P(y_t|y_1,y_2,…,y_{t-1},C)
$$

应用场景：机器翻译（NMT）

4.3.2 Attention机制

4.3.2.1 长句子问题

对于长句子，Seq2Seq模型的性能会下降，无法做到准确翻译。
句子非常长时，BLEU（Bilingual Evaluation Understudy）评价得分会很低

本质原因：在Encoder-Decoder结构中，Encoder把所有的输入序列都编码成一个统一的语义特征$C$再解码，$C$中必须包含原始序列中的所有信息，它的长度就成了模型性能的瓶颈。
当需要翻译的句子很长时，一个$C$可能存不下那么多信息，就会造成翻译精度的下降。

4.3.2.2 Attention机制

把Encoder的所有隐层输出$s_1,s_2,…,s_T$都保留下来，不再只保留最后一个隐层输出$C$
将这些信息提供给Decoder

Attention机制

4.3.2.3 Attention机制的计算

假设Encoder的时刻为$t$，Decoder的时刻为$t’$

$c_{t’}=\sum_{t=1}^T \alpha_{t’t}s_t$
- $\alpha_{t’t}$：参数，训练得到，表示Decoder的$t’$时刻对Encoder的$t$时刻的注意力权重
- 理解：Encoder的每个时刻加权求和，得到Decoder的$t’$时刻的输入
- $c_4=\alpha_{41}s_1+\alpha_{42}s_2+…+\alpha_{4T}s_T$
$\alpha_{t’t}$的$N$个权重系数的由来
- 权重系数通过Softmax函数得到，$\alpha_{t’t}=\frac{exp(e_{t’t})}{\sum_{k=1}^T exp(e_{t’k})}$
- $e_{t’t}=g(s_{t’-1},h_t)=v^T \tanh(W_ss+W_hh)$
  - $e_{t’t}$：由t时刻的编码器隐层状态输出和t’-1时刻的解码器隐层状态输出计算得到的一个值
  - s为Decoder的隐层输出，h为Encoder的隐层输出
  - $W_s, W_h, v$：参数，训练得到